ARTICLE AD BOX
In today’s data-driven world, businesslike geospatial indexing is important for applications ranging from ride-sharing and logistics to biology monitoring and disaster response. Uber’s H3, a powerful open-source spatial indexing system, provides a unsocial hexagonal grid-based solution that enables seamless geospatial study and accelerated query execution. Unlike accepted rectangular grid systems, H3’s hierarchical hexagonal tiling ensures azygous spatial coverage, amended adjacency properties, and reduced distortion. This guideline explores H3’s halfway concepts, installation, functionality, usage cases, and champion practices to thief developers and information scientists leverage its afloat potential.
Learning Objectives
- Understand nan fundamentals of Uber’s H3 spatial indexing strategy and its advantages complete accepted grid systems.
- Learn really to instal and group up H3 for geospatial applications successful Python, JavaScript, and different languages.
- Explore H3’s hierarchical hexagonal grid building and its benefits for spatial accuracy and indexing.
- Gain hands-on acquisition pinch halfway H3 functions for illustration neighbour lookup, polygon indexing, and region calculations.
- Discover real-world applications of H3, including machine learning, disaster response, and biology monitoring.
This article was published arsenic a portion of the Data Science Blogathon.
What is Uber H3?
Uber H3 is an open-source, hexagonal hierarchical spatial indexing strategy developed by Uber. It is designed to efficiently partition and scale geographic space, enabling precocious geospatial analysis, accelerated queries, and seamless visualization. Unlike accepted grid systems that usage quadrate aliases rectangular tiles, H3 utilizes hexagons, which supply superior spatial relationships, amended adjacency properties, and minimize distortion erstwhile representing nan Earth’s surface.
Why Uber Developed H3?
Uber developed H3 to lick cardinal challenges successful geospatial computing, peculiarly successful ride-sharing, logistics, and location-based services. Traditional approaches based connected latitude-longitude coordinates, rectangular grids, aliases QuadTrees often suffer from inconsistencies successful resolution, inefficient spatial queries, and mediocre practice of real-world spatial relationships. H3 addresses these limitations by:
- Providing a uniform, hierarchical hexagonal grid that allows for seamless scalability crossed different resolutions.
- Enabling accelerated nearest-neighbour lookups and businesslike spatial indexing for ride-demand forecasting, routing, and proviso distribution.
- Supporting spatial queries and geospatial clustering pinch precocious accuracy and minimal computational overhead.
Today, H3 is wide utilized successful applications beyond Uber, including biology monitoring, geospatial analytics, and geographic accusation systems (GIS).
What is Spatial Indexing?
Spatial indexing is simply a method utilized to building and shape geospatial information efficiently, allowing for accelerated spatial queries and improved information retrieval performance. It is important for tasks specified as:
- Nearest neighbour search
- Geospatial clustering
- Efficient geospatial joins
- Region-based filtering
H3 enhances spatial indexing by utilizing a hexagonal grid system, which improves spatial accuracy, provides amended adjacency properties, and reduces distortions recovered successful accepted grid-based systems.
Installation Guide (Python, JavaScript, Go, C, etc.)
Setting Up H3 successful a Development Environment
Let america now group up H3 successful a improvement situation below:
# Create a virtual environment python -m venv h3_env source h3_env/bin/activate # Linux/macOS h3_env\Scripts\activate # Windows # Install dependencies pip instal h3 geopandas matplotlibData Structure and Hierarchical Indexing
Below we will understand information building and hierarchical indexing successful detail:
Hexagonal Grid System
H3’s hexagonal grid partitions Earth into 122 guidelines cells (resolution 0), comprising 110 hexagons and 12 pentagons to approximate spherical geometry. Each compartment undergoes hierarchical subdivision using aperture 7 partitioning, wherever each genitor hexagon contains 7 kid cells astatine nan adjacent solution level. This creates 16 solution levels (0-15) pinch exponentially decreasing compartment sizes:
| 0 | 1,107.712 | 4,250,546 | – |
| 5 | 8.544 | 252.903 | 16,807 |
| 9 | 0.174 | 0.105 | 40,353,607 |
| 15 | 0.0005 | 0.0000009 | 7^15 ≈ 4.7e12 |
The codification beneath demonstrates H3’s hierarchical hexagonal grid strategy :
import folium import h3 base_cell = '8001fffffffffff' # Resolution 0 pentagon children = h3.cell_to_children(base_cell, res=1) # Create a representation centered astatine nan halfway of nan guidelines hexagon base_center = h3.cell_to_latlng(base_cell) GeoSpatialMap = folium.Map(location=[base_center[0], base_center[1]], zoom_start=9) # Function to get hexagon boundaries def get_hexagon_bounds(h3_address): boundaries = h3.cell_to_boundary(h3_address) # Folium expects coordinates successful [lat, lon] format return [[lat, lng] for lat, lng successful boundaries] # Add guidelines hexagon folium.Polygon( locations=get_hexagon_bounds(base_cell), color='red', fill=True, weight=2, popup=f'Base: {base_cell}' ).add_to(GeoSpatialMap) # Add children hexagons for kid successful children: folium.Polygon( locations=get_hexagon_bounds(child), color='blue', fill=True, weight=1, popup=f'Child: {child}' ).add_to(GeoSpatialMap) GeoSpatialMap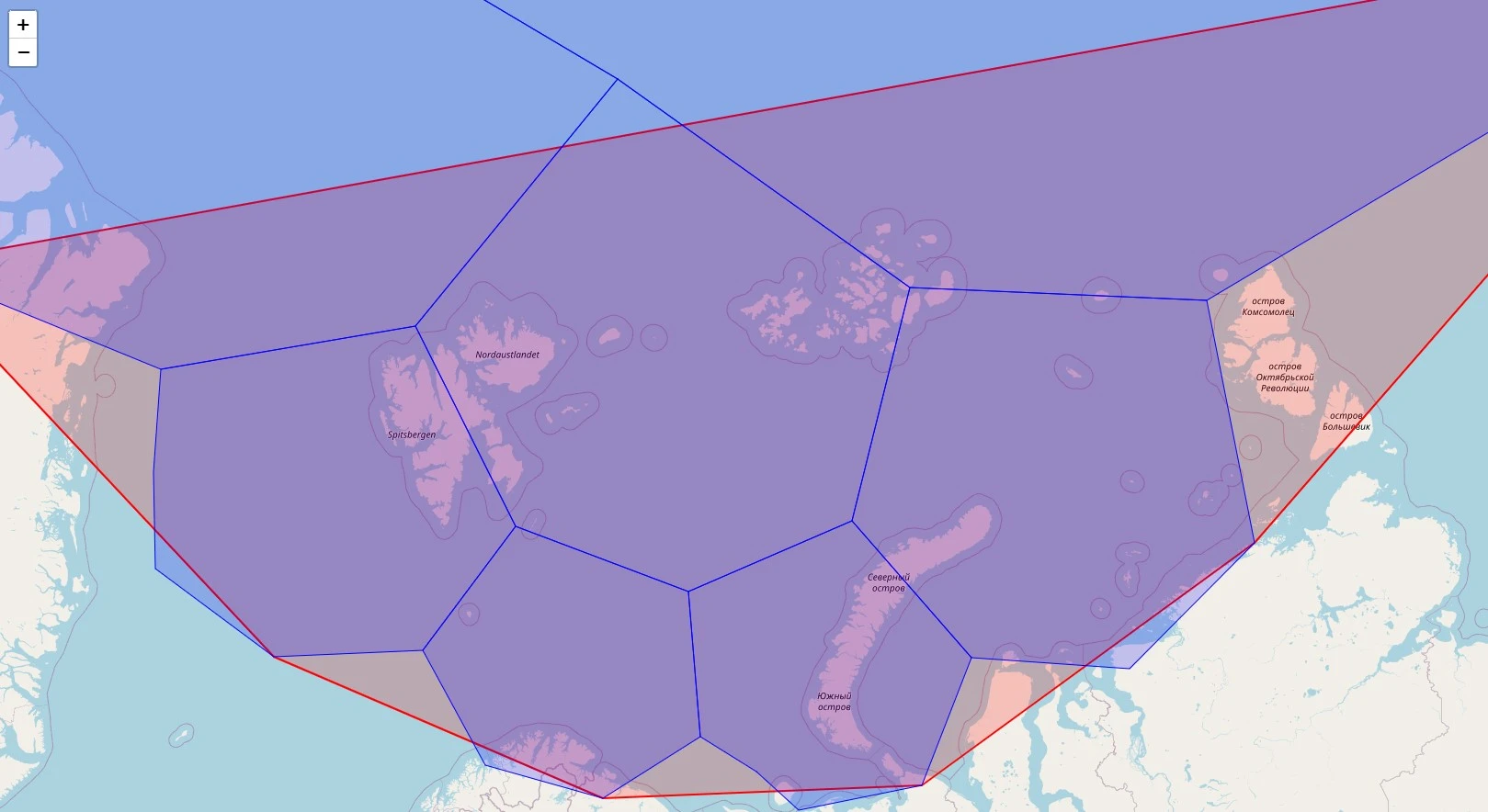
Resolution Levels and Hierarchical Indexing
The hierarchical indexing building enables multi-resolution study done parent-child relationships. H3 supports hierarchical solution levels (from 0 to 15), allowing information to beryllium indexed astatine different granularities.
The fixed codification beneath shows this relationship:
delhi_cell = h3.latlng_to_cell(28.6139, 77.2090, 9) # New Delhi coordinates # Traverse level upwards parent = h3.cell_to_parent(delhi_cell, res=8) print(f"Parent astatine res 8: {parent}") # Traverse level downwards children = h3.cell_to_children(parent, res=9) print(f"Contains {len(children)} children") # Create a caller representation centered connected New Delhi delhi_map = folium.Map(location=[28.6139, 77.2090], zoom_start=15) # Add nan genitor hexagon (resolution 8) folium.Polygon( locations=get_hexagon_bounds(parent), color='red', fill=True, weight=2, popup=f'Parent: {parent}' ).add_to(delhi_map) # Add each children hexagons (resolution 9) for child_cell successful children: colour = 'yellow' if child_cell == delhi_cell other 'blue' folium.Polygon( locations=get_hexagon_bounds(child_cell), color=color, fill=True, weight=1, popup=f'Child: {child_cell}' ).add_to(delhi_map) delhi_map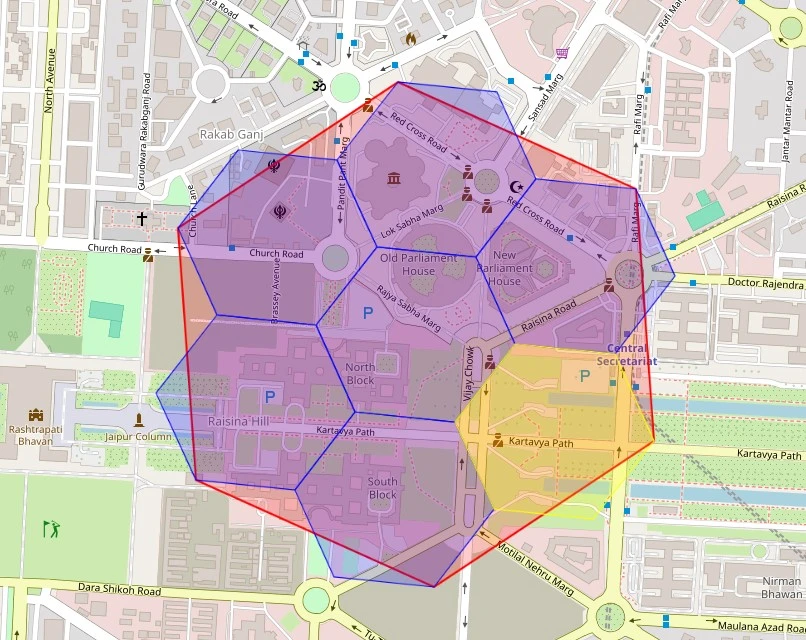
H3 Index Encoding
The H3 scale encodes geospatial information into a 64-bit unsigned integer (commonly represented arsenic a 15-character hexadecimal drawstring like ‘89283082837ffff’). H3 indexes person nan pursuing architecture:
| Mode and Resolution | Reserved | Base Cell | Child digits |
We tin understand nan encoding process by nan pursuing codification below:
import h3 # Convert coordinates to H3 scale (resolution 9) lat, lng = 37.7749, -122.4194 # San Francisco h3_index = h3.latlng_to_cell(lat, lng, 9) print(h3_index) # '89283082803ffff' # Deconstruct scale components ## Get nan resolution resolution = h3.get_resolution(h3_index) print(f"Resolution: {resolution}") # Output: 9 # Get nan guidelines compartment number base_cell = h3.get_base_cell_number(h3_index) print(f"Base cell: {base_cell}") # Output: 20 # Check if its a pentagon is_pentagon = h3.is_pentagon(h3_index) print(f"Is pentagon: {is_pentagon}") # Output: False # Get nan icosahedron face face = h3.get_icosahedron_faces(h3_index) print(f"Face number: {face}") # Output: [7] # Get nan kid cells child_cells = h3.cell_to_children(h3.cell_to_parent(h3_index, 8), 9) print(f"child cells: {child_cells}") # Output: ['89283082803ffff', '89283082807ffff', '8928308280bffff', '8928308280fffff', # '89283082813ffff', '89283082817ffff', '8928308281bffff']Core Functions
Apart from nan Hierarchical Indexing, immoderate of nan different Core functions of H3 are arsenic follows:
- Neighbor Lookup & Traversal
- Polygon to H3 Indexing
- H3 Grid Distance and K-Ring
Neighbor Lookup andTraversal
Neighbor lookup traversal refers to identifying and navigating betwixt adjacent cells in Uber’s H3 hexagonal grid system. This enables spatial queries for illustration “find each cells wrong a radius of k steps” from a target cell. This conception tin beryllium understood from nan codification below:
import h3 # Define latitude, longitude for Kolkata lat, lng = 22.5744, 88.3629 resolution = 9 h3_index = h3.latlng_to_cell(lat, lng, resolution) print(h3_index) # e.g., '89283082837ffff' # Find each neighbors wrong 1 grid step neighbors = h3.grid_disk(h3_index, k=1) print(len(neighbors)) # 7 (6 neighbors + nan original cell) # Check separator adjacency is_neighbor = h3.are_neighbor_cells(h3_index, neighbors[0]) print(is_neighbor) # True aliases FalseTo make nan visualization of this we tin simply usage nan codification fixed below:
import h3 import folium # Define latitude, longitude for Kolkata lat, lng = 22.5744, 88.3629 resolution = 9 # H3 resolution # Convert lat/lng to H3 index h3_index = h3.latlng_to_cell(lat, lng, resolution) # Get neighboring hexagons neighbors = h3.grid_disk(h3_index, k=1) # Initialize representation centered astatine nan fixed location m = folium.Map(location=[lat, lng], zoom_start=12) # Function to adhd hexagons to nan map def add_hexagon(h3_index, color): """ Adds an H3 hexagon to nan folium representation """ bound = h3.cell_to_boundary(h3_index) # Convert to [lat, lng] format for folium bound = [[lat, lng] for lat, lng successful boundary] folium.Polygon( locations=boundary, color=color, fill=True, fill_color=color, fill_opacity=0.5 ).add_to(m) # Add cardinal hexagon successful red add_hexagon(h3_index, "red") # Add neighbour hexagons successful blue for neighbour successful neighbors: if neighbour != h3_index: # Avoid recoloring nan center add_hexagon(neighbor, "blue") # Display nan map m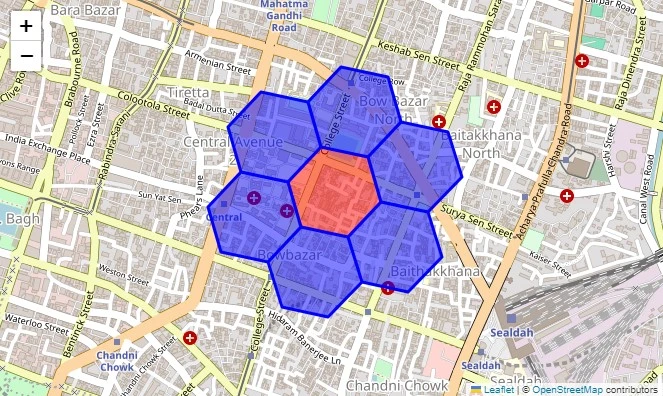
Use cases of Neighbor Lookup & Traversal are arsenic follows:
- Ride Sharing: Find disposable drivers wrong a 5-minute thrust radius.
- Spatial Aggregation: Calculate full rainfall successful cells wrong 10 km of a flood zone.
- Machine Learning: Generate vicinity features for request prediction models.
Polygon to H3 Indexing
Converting a polygon to H3 indexes involves identifying each hexagonal cells astatine a specified solution that fully aliases partially intersect with nan polygon. This is captious for spatial operations for illustration aggregating information wrong geographic boundaries. This could beryllium understood from nan fixed codification below:
import h3 # Define a polygon (e.g., San Francisco bounding box) polygon_coords = h3.LatLngPoly( [(37.708, -122.507), (37.708, -122.358), (37.832, -122.358), (37.832, -122.507)] ) # Convert polygon to H3 cells (resolution 9) resolution = 9 cells = h3.polygon_to_cells(polygon_coords, res=resolution) print(f"Total cells: {len(cells)}") # Output: ~ 1651To visualize this we tin travel nan fixed codification below:
import h3 import folium from h3 import LatLngPoly # Define a bounding polygon for Kolkata kolkata_coords = LatLngPoly([ (22.4800, 88.2900), # Southwest corner (22.4800, 88.4200), # Southeast corner (22.5200, 88.4500), # East (22.5700, 88.4500), # Northeast (22.6200, 88.4200), # North (22.6500, 88.3500), # Northwest (22.6200, 88.2800), # West (22.5500, 88.2500), # Southwest (22.5000, 88.2700) # Return to starting area ]) # Add much bound coordinates for much circumstantial map # Convert polygon to H3 cells resolution = 9 cells = h3.polygon_to_cells(kolkata_coords, res=resolution) # Create a Folium representation centered astir Kolkata kolkata_map = folium.Map(location=[22.55, 88.35], zoom_start=12) # Add each H3 compartment arsenic a polygon for compartment successful cells: boundaries = h3.cell_to_boundary(cell) # Convert to [lat, lng] format for folium boundaries = [[lat, lng] for lat, lng successful boundaries] folium.Polygon( locations=boundaries, color='blue', weight=1, fill=True, fill_opacity=0.4, popup=cell ).add_to(kolkata_map) # Show map kolkata_map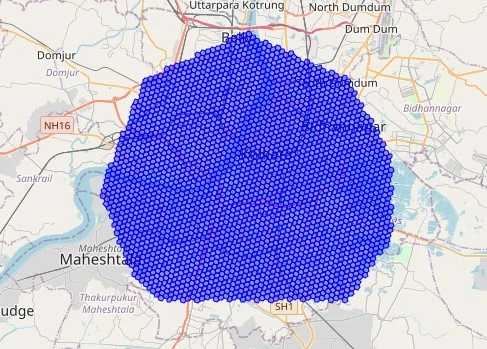
H3 Grid Distance and K-Ring
Grid distance measures nan minimum number of steps required to traverse from 1 H3 compartment to another, moving done adjacent cells. Unlike geographical distance, it’s a topological metric based connected hexagonal grid connectivity. And we should support successful mind that higher resolutions output smaller steps truthful nan grid region would beryllium larger.
import h3 from h3 import latlng_to_cell # Define 2 H3 cells astatine solution 9 cell_a = latlng_to_cell(37.7749, -122.4194, 9) # San Francisco cell_b = latlng_to_cell(37.3382, -121.8863, 9) # San Jose # Calculate grid region distance = h3.grid_distance(cell_a, cell_b) print(f"Grid distance: {distance} steps") # Output: Grid distance: 220 steps (approx)We tin visualize this pinch nan pursuing fixed code:
import h3 import folium from h3 import latlng_to_cell from shapely.geometry import Polygon # Function to get H3 polygon boundary def get_h3_polygon(h3_index): bound = h3.cell_to_boundary(h3_index) return [(lat, lon) for lat, lon successful boundary] # Define 2 H3 cells astatine solution 6 cell_a = latlng_to_cell(37.7749, -122.4194, 6) # San Francisco cell_b = latlng_to_cell(37.3382, -121.8863, 6) # San Jose # Get hexagon boundaries polygon_a = get_h3_polygon(cell_a) polygon_b = get_h3_polygon(cell_b) # Compute grid distance distance = h3.grid_distance(cell_a, cell_b) # Create a folium representation centered betwixt nan 2 locations map_center = [(37.7749 + 37.3382) / 2, (-122.4194 + -121.8863) / 2] m = folium.Map(location=map_center, zoom_start=9) # Add H3 hexagons to nan map folium.Polygon(locations=polygon_a, color='blue', fill=True, fill_opacity=0.4, popup="San Francisco (H3)").add_to(m) folium.Polygon(locations=polygon_b, color='red', fill=True, fill_opacity=0.4, popup="San Jose (H3)").add_to(m) # Add markers for nan halfway points folium.Marker([37.7749, -122.4194], popup="San Francisco").add_to(m) folium.Marker([37.3382, -121.8863], popup="San Jose").add_to(m) # Display distance folium.Marker(map_center, popup=f"H3 Grid Distance: {distance} steps", icon=folium.Icon(color='green')).add_to(m) # Show nan map m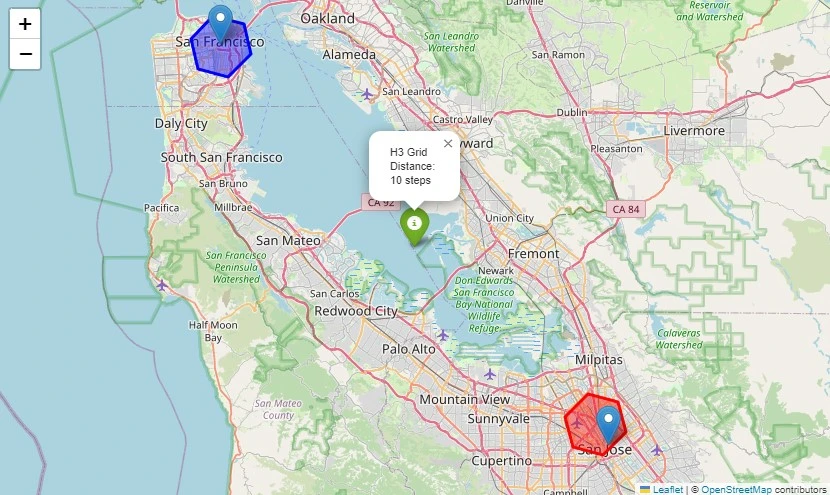
And K-Ring (or grid disk) successful H3 refers to each hexagonal cells within k grid steps from a cardinal cell. This includes:
- The cardinal compartment itself (at measurement 0).
- Immediate neighbors (step 1).
- Cells astatine progressively larger distances up to `k` steps.
This tin beryllium visualized from nan crippled fixed below:
import h3 import matplotlib.pyplot arsenic plt from shapely.geometry import Polygon import geopandas arsenic gpd # Define cardinal constituent (latitude, longitude) for San Francisco [1] lat, lng = 37.7749, -122.4194 resolution = 9 # Choose solution (e.g., 9) [1] # Obtain cardinal H3 compartment scale for nan fixed constituent [1] center_h3 = h3.latlng_to_cell(lat, lng, resolution) print("Central H3 cell:", center_h3) # Example output: '89283082837ffff' # Define k worth (number of grid steps) for nan k-ring [1] k = 2 # Generate k-ring of cells: each cells wrong k grid steps of centerH3 [1] k_ring_cells = h3.grid_disk(center_h3, k) print("Total k-ring cells:", len(k_ring_cells)) # For a modular hexagon (non-pentagon), k=2 typically returns 19 cells: # 1 (central cell) + 6 (neighbors astatine region 1) + 12 (neighbors astatine region 2) # Convert each H3 compartment into a Shapely polygon for visualization [1][6] polygons = [] for compartment successful k_ring_cells: # Get nan compartment bound arsenic a database of (lat, lng) pairs; geo_json=True returns successful [lat, lng] bound = h3.cell_to_boundary(cell) # Swap to (lng, lat) because Shapely expects (x, y) poly = Polygon([(lng, lat) for lat, lng successful boundary]) polygons.append(poly) # Create a GeoDataFrame for plotting nan hexagonal cells [2] gdf = gpd.GeoDataFrame({'h3_index': list(k_ring_cells)}, geometry=polygons) # Plot nan boundaries of nan k-ring cells utilizing Matplotlib [2][6] fig, ax = plt.subplots(figsize=(8, 8)) gdf.boundary.plot(ax=ax, color='blue', lw=1) # Highlight nan cardinal compartment by plotting its bound successful reddish [1] central_boundary = h3.cell_to_boundary(center_h3) central_poly = Polygon([(lng, lat) for lat, lng successful central_boundary]) gpd.GeoSeries([central_poly]).boundary.plot(ax=ax, color='red', lw=2) # Set crippled labels and title for clear visualization ax.set_title("H3 K-Ring Visualization (k = 2)") ax.set_xlabel("Longitude") ax.set_ylabel("Latitude") plt.show()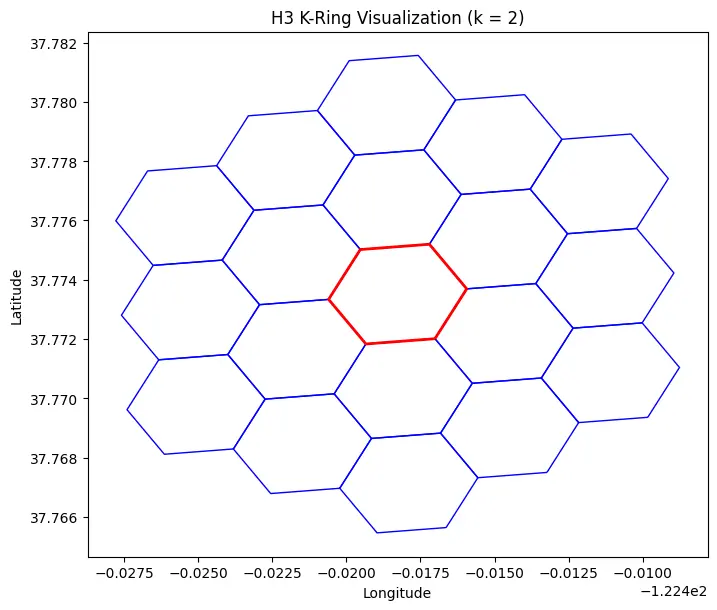
Use Cases
While nan usage cases of H3 are only constricted to one’s creativity, present are fewer examples of it :
Efficient Geo-Spatial Queries
H3 excels astatine optimizing location-based queries, specified arsenic counting points of liking (POIs) wrong move geographic boundaries.
In this usage case, we show really H3 tin beryllium applied to analyse and visualize thrust pickup density successful San Francisco utilizing Python. To simulate real-world thrust data, we make random GPS coordinates centered astir San Francisco. We besides delegate each thrust a random timestamp wrong nan past week to create a realistic dataset. Each ride’s latitude and longitude are converted into an H3 scale astatine solution 10, a fine-grained hexagonal grid that helps successful spatial aggregation. To analyse section thrust pickup density, we prime a target H3 compartment and retrieve each adjacent cells wrong 2 hexagonal rings utilizing h3.grid_disk. To visualize nan spatial distribution of pickups, we overlay nan H3 hexagons onto a Folium map.
Code Implementation
The execution codification is fixed below:
import pandas arsenic pd import h3 import folium import matplotlib.pyplot arsenic plt import numpy arsenic np from datetime import datetime, timedelta import random # Create sample GPS information astir San Francisco # Center coordinates for San Francisco center_lat, center_lng = 37.7749, -122.4194 # Generate synthetic thrust data num_rides = 1000 np.random.seed(42) # For reproducibility # Generate random coordinates astir San Francisco lats = np.random.normal(center_lat, 0.02, num_rides) # Normal distribution astir center lngs = np.random.normal(center_lng, 0.02, num_rides) # Generate timestamps for nan past week start_time = datetime.now() - timedelta(days=7) timestamps = [start_time + timedelta(minutes=random.randint(0, 10080)) for _ successful range(num_rides)] timestamp_strs = [ts.strftime('%Y-%m-%d %H:%M:%S') for ts successful timestamps] # Create DataFrame rides = pd.DataFrame({ 'lat': lats, 'lng': lngs, 'timestamp': timestamp_strs }) # Convert coordinates to H3 indexes (resolution 10) rides["h3"] = rides.apply( lambda row: h3.latlng_to_cell(row["lat"], row["lng"], 10), axis=1 ) # Count pickups per cell pickup_counts = rides["h3"].value_counts().reset_index() pickup_counts.columns = ["h3", "counts"] # Query pickups wrong a circumstantial compartment and its neighbors target_cell = h3.latlng_to_cell(37.7749, -122.4194, 10) neighbors = h3.grid_disk(target_cell, k=2) local_pickups = pickup_counts[pickup_counts["h3"].isin(neighbors)] # Visualize nan spatial query results map_center = h3.cell_to_latlng(target_cell) m = folium.Map(location=map_center, zoom_start=15) # Function to get hexagon boundaries def get_hexagon_bounds(h3_address): boundaries = h3.cell_to_boundary(h3_address) return [[lat, lng] for lat, lng successful boundaries] # Add target cell folium.Polygon( locations=get_hexagon_bounds(target_cell), color='red', fill=True, weight=2, popup=f'Target Cell: {target_cell}' ).add_to(m) # Color standard for counts max_count = local_pickups["counts"].max() min_count = local_pickups["counts"].min() # Add neighbour cells pinch colour strength based connected pickup counts for _, statement successful local_pickups.iterrows(): if row["h3"] != target_cell: # Calculate colour strength based connected count strength = (row["counts"] - min_count) / (max_count - min_count) if max_count > min_count other 0.5 colour = f'#{int(255*(1-intensity)):02x}{int(200*(1-intensity)):02x}ff' folium.Polygon( locations=get_hexagon_bounds(row["h3"]), color=color, fill=True, fill_opacity=0.7, weight=1, popup=f'Cell: {row["h3"]}<br>Pickups: {row["counts"]}' ).add_to(m) # Create a heatmap visualization pinch matplotlib plt.figure(figsize=(12, 8)) plt.title("H3 Grid Heatmap of Ride Pickups") # Create a scatter crippled for cells, size based connected pickup counts for idx, statement successful local_pickups.iterrows(): halfway = h3.cell_to_latlng(row["h3"]) plt.scatter(center[1], center[0], s=row["counts"]/2, c=row["counts"], cmap='viridis', alpha=0.7) plt.colorbar(label='Number of Pickups') plt.xlabel('Longitude') plt.ylabel('Latitude') plt.grid(True) # Display some visualizations m # Display nan folium map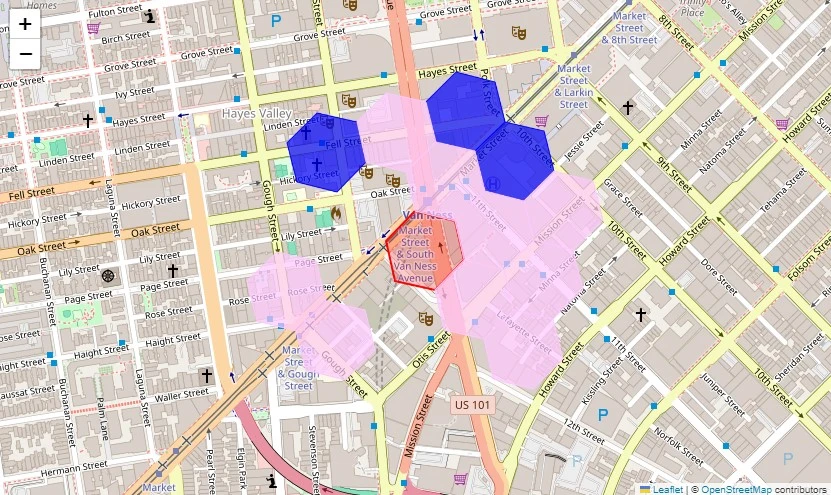
The supra illustration highlights really H3 tin beryllium leveraged for spatial study successful municipality mobility. By converting earthy GPS coordinates into a hexagonal grid, we tin efficiently analyse thrust density, observe hotspots, and visualize information successful an insightful manner. H3’s elasticity successful handling different resolutions makes it a valuable instrumentality for geospatial analytics successful ride-sharing, logistics, and municipality readying applications.
Combining H3 pinch Machine Learning
H3 has been mixed pinch Machine Learning to lick galore existent world problems. Uber reduced ETA prediction errors by 22% utilizing H3-based ML models while Toulouse, France, utilized H3 + ML to optimize motorcycle lane placement, expanding ridership by 18%.
In this usage case, we show really H3 tin beryllium applied to analyse and foretell postulation congestion successful San Francisco utilizing humanities GPS thrust information and instrumentality learning techniques. To simulate real-world postulation conditions, we make random GPS coordinates centered astir San Francisco. Each thrust is assigned a random timestamp wrong nan past week, on pinch a randomly generated velocity value. Each ride’s latitude and longitude are converted into an H3 scale astatine solution 10, enabling spatial aggregation and analysis. We extract features from a sample compartment and its neighboring cells wrong 2 hexagonal rings to analyse section postulation conditions. To foretell postulation congestion, we usage an LSTM-based heavy learning model. The exemplary is designed to process humanities postulation information and foretell congestion probabilities. Using nan trained model, we tin foretell nan probability of congestion for a fixed cell.
Code Implementation
The execution codification is fixed beneath :
import h3 import pandas arsenic pd import numpy arsenic np from datetime import datetime, timedelta import random import tensorflow arsenic tf from tensorflow.keras.layers import LSTM, Conv1D, Dense # Create sample GPS information astir San Francisco center_lat, center_lng = 37.7749, -122.4194 num_rides = 1000 np.random.seed(42) # For reproducibility # Generate random coordinates astir San Francisco lats = np.random.normal(center_lat, 0.02, num_rides) lngs = np.random.normal(center_lng, 0.02, num_rides) # Generate timestamps for nan past week start_time = datetime.now() - timedelta(days=7) timestamps = [start_time + timedelta(minutes=random.randint(0, 10080)) for _ successful range(num_rides)] timestamp_strs = [ts.strftime('%Y-%m-%d %H:%M:%S') for ts successful timestamps] # Generate random velocity data speeds = np.random.uniform(5, 60, num_rides) # Speed successful km/h # Create DataFrame gps_data = pd.DataFrame({ 'lat': lats, 'lng': lngs, 'timestamp': timestamp_strs, 'speed': speeds }) # Convert coordinates to H3 indexes (resolution 10) gps_data["h3"] = gps_data.apply( lambda row: h3.latlng_to_cell(row["lat"], row["lng"], 10), axis=1 ) # Convert timestamp drawstring to datetime objects gps_data["timestamp"] = pd.to_datetime(gps_data["timestamp"]) # Aggregate velocity and count per compartment per 5-minute interval agg_data = gps_data.groupby(["h3", pd.Grouper(key="timestamp", freq="5T")]).agg( avg_speed=("speed", "mean"), vehicle_count=("h3", "count") ).reset_index() # Example: Use a compartment from our existing dataset sample_cell = gps_data["h3"].iloc[0] neighbors = h3.grid_disk(sample_cell, 2) def get_kring_features(cell, k=2): neighbors = h3.grid_disk(cell, k) return {f"neighbor_{i}": neighbour for i, neighbour successful enumerate(neighbors)} # Placeholder usability for characteristic extraction def fetch_features(neighbors, agg_data): # In a existent implementation, this would fetch humanities information for nan neighbors # This is conscionable a simplified illustration that returns random data return np.random.rand(1, 6, len(neighbors)) # 1 sample, 6 timesteps, features per neighbor # Define a skeleton exemplary architecture def create_model(input_shape): exemplary = tf.keras.Sequential([ LSTM(64, return_sequences=True, input_shape=input_shape), LSTM(32), Dense(16, activation='relu'), Dense(1, activation='sigmoid') ]) model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy']) return model # Prediction usability (would usage a trained exemplary successful practice) def predict_congestion(cell, model, agg_data): # Fetch neighbour cells neighbors = h3.grid_disk(cell, k=2) # Get humanities information for neighbors features = fetch_features(neighbors, agg_data) # Predict return model.predict(features)[0][0] # Create a skeleton exemplary (not trained) input_shape = (6, 19) # 6 clip steps, 19 features (for k=2 neighbors) model = create_model(input_shape) # Print accusation astir what would hap successful a existent prediction print(f"Sample cell: {sample_cell}") print(f"Number of neighboring cells (k=2): {len(neighbors)}") print("Model summary:") model.summary() # In practice, you would train nan exemplary earlier utilizing it for predictions # This would conscionable show what a prediction telephone would look like: congestion_prob = predict_congestion(sample_cell, model, agg_data) print(f"Congestion probability: {congestion_prob:.2%}") # illustration output- Congestion Probability: 49.09%This illustration demonstrates really H3 tin beryllium leveraged for spatial study and postulation prediction. By converting GPS information into hexagonal grids, we tin efficiently analyse postulation patterns, extract meaningful insights from neighboring regions, and usage heavy learning to foretell congestion successful existent time. This attack tin beryllium applied to smart metropolis planning, ride-sharing optimizations, and intelligent postulation guidance systems.
Disaster Response and Environmental Monitoring
Flood events represent one of nan most common earthy disasters requiring contiguous consequence and assets allocation. H3 tin importantly amended flood consequence efforts by integrating various information sources including flood area maps, organization density, building infrastructure, and real-time h2o level readings.
The pursuing Python implementation demonstrates how to usage H3 for flood consequence study by integrating flooded area data with building infrastructure information:
import h3 import folium import pandas arsenic pd import numpy arsenic np from folium.plugins import MarkerCluster # Create sample buildings dataset np.random.seed(42) num_buildings = 50 # Create buildings astir San Francisco center_lat, center_lng = 37.7749, -122.4194 building_types = ['residential', 'commercial', 'hospital', 'school', 'government'] building_weights = [0.6, 0.2, 0.1, 0.07, 0.03] # Probability weights # Generate building data buildings_df = pd.DataFrame({ 'lat': np.random.normal(center_lat, 0.005, num_buildings), 'lng': np.random.normal(center_lng, 0.005, num_buildings), 'type': np.random.choice(building_types, size=num_buildings, p=building_weights), 'capacity': np.random.randint(10, 1000, num_buildings) }) # Add H3 scale astatine solution 10 buildings_df['h3_index'] = buildings_df.apply( lambda row: h3.latlng_to_cell(row['lat'], row['lng'], 10), axis=1 ) # Create immoderate flood cells (let's usage immoderate cells wherever buildings are located) # Taking a fewer cells wherever buildings are located to simulate a flood zone flood_cells = set(buildings_df['h3_index'].sample(10)) # Create a representation centered astatine nan mean of our coordinates center_lat = buildings_df['lat'].mean() center_lng = buildings_df['lng'].mean() flood_map = folium.Map(location=[center_lat, center_lng], zoom_start=16) # Function to get hexagon boundaries for folium def get_hexagon_bounds(h3_address): boundaries = h3.cell_to_boundary(h3_address) # Folium expects coordinates successful [lat, lng] format return [[lat, lng] for lat, lng successful boundaries] # Add flood area cells for compartment successful flood_cells: folium.Polygon( locations=get_hexagon_bounds(cell), color='blue', fill=True, fill_opacity=0.4, weight=2, popup=f'Flood Cell: {cell}' ).add_to(flood_map) # Add building markers for idx, statement successful buildings_df.iterrows(): # Set colour based connected if building is affected if row['h3_index'] successful flood_cells: colour = 'red' icon = 'warning' if row['type'] successful ['hospital', 'school'] other 'info-sign' prefix = 'glyphicon' else: colour = 'green' icon = 'home' prefix = 'glyphicon' # Create marker pinch popup showing building details folium.Marker( location=[row['lat'], row['lng']], popup=f"Building Type: {row['type']}<br>Capacity: {row['capacity']}", tooltip=f"{row['type']} (Capacity: {row['capacity']})", icon=folium.Icon(color=color, icon=icon, prefix=prefix) ).add_to(flood_map) # Add a fable arsenic an HTML element legend_html = ''' <div style="position: fixed; bottom: 50px; left: 50px; width: 200px; height: 120px; border:2px coagulated grey; z-index:9999; font-size:14px; background-color:white; padding: 10px; border-radius: 5px;"> <b>Flood Impact Analysis</b> <br> <i class="glyphicon glyphicon-stop" style="color:blue"></i> Flood Zone <br> <i class="glyphicon glyphicon-home" style="color:green"></i> Safe Buildings <br> <i class="glyphicon glyphicon-info-sign" style="color:red"></i> Affected Buildings <br> <i class="glyphicon glyphicon-warning-sign" style="color:red"></i> Critical Facilities <br> </div> ''' flood_map.get_root().html.add_child(folium.Element(legend_html)) # Display nan map flood_map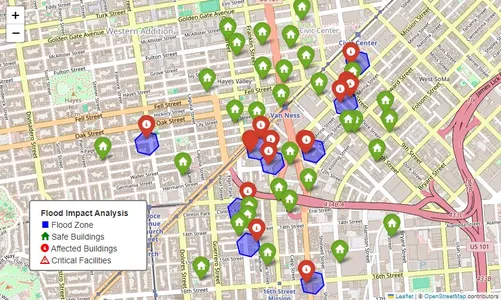
This codification provides an businesslike method for visualizing and analyzing flood impacts utilizing H3 spatial indexing and Folium mapping. By integrating spatial information clustering and interactive visualization, it enhances disaster consequence readying and municipality consequence guidance strategies. This attack tin beryllium extended to different geospatial challenges, specified arsenic wildfire consequence appraisal aliases proscription planning.
Strengths and Weaknesses of H3
The pursuing array provides a elaborate study of H3’s advantages and limitations based connected manufacture implementations and method evaluations:
| Geometry Properties | Hexagonal cells supply azygous region metrics pinch equidistant neighbors. Better approximation of circles than square/rectangular grids. Minimizes some area and style distortion globally | Cannot wholly disagreement Earth into hexagons, requires 12 pentagon cells that create irregular adjacency patterns. Not a existent equal-area system, contempt aiming for “roughly equal-ish” areas |
| Hierarchical Structure | Efficiently changes precision (resolution) levels arsenic needed. Compact 64-bit addresses for each resolutions- Parent-child character pinch nary shared parents. | Hierarchical nesting betwixt resolutions isn’t perfect. Tiny discontinuities (gaps/overlaps) tin hap astatine adjacent scales. Problematic for usage cases requiring nonstop containment (e.g., parcel data) |
| Performance | H3-centric approaches tin beryllium up to 90x little costly than geometry-centric operations. Significantly enhances processing ratio pinch ample dataset. Fast calculations betwixt predictable cells successful grid system | Processing ample areas astatine precocious resolutions requires important computational resources. Trade-off betwixt precision and capacity – higher resolutions devour much resources. |
| Spatial Analysis | Multi-resolution study from vicinity to location scales. Standardized format for integrating heterogeneous information sources. Uniform adjacency relationships simplify vicinity searches | Polygon sum is approximate pinch imaginable gaps astatine boundaries. Precision limitations limited connected chosen solution level. Special handling required for polygon intersections |
| Implementation | Simple API pinch built-in utilities (geofence polyfill, hexagon compaction, GeoJSON output)- Well-suited for parallelized execution. Cell IDs tin beryllium utilized arsenic columns successful modular SQL functions. | Handling pentagon cells requires specialized code. Adapting existing workflows to H3 tin beryllium complex. Data value limitations impact study accuracy |
| Applications | Optimized for: geospatial analytics, mobility analysis, logistics, transportation services, telecoms, security consequence assessment, and biology monitoring. | Less suitable for applications requiring nonstop bound definitions. May not beryllium optimal for specialized cartographic purposes. Can impact computational complexity for real-time applications pinch constricted resources. |
Conclusion
Uber’s H3 spatial indexing strategy is simply a powerful instrumentality for geospatial analysis, offering a hexagonal grid building that enables businesslike spatial queries, multi-resolution analysis, and seamless integration pinch modern information workflows. Its strengths dishonesty successful its azygous geometry, hierarchical design, and expertise to grip large-scale datasets pinch velocity and precision. From ride-sharing optimization to disaster consequence and biology monitoring, H3 has proven its versatility crossed industries.
However, for illustration immoderate technology, H3 has limitations, specified arsenic handling pentagon cells, approximating polygon boundaries, and computational demands astatine precocious resolutions. By knowing its strengths and weaknesses, developers tin leverage H3 efficaciously for applications requiring scalable and meticulous geospatial insights.
As geospatial exertion evolves, H3’s open-source ecosystem will apt spot further enhancements, including integration pinch instrumentality learning models, real-time analytics, and 3D spatial indexing. H3 is not conscionable a instrumentality but a instauration for building smarter geospatial solutions successful an progressively data-driven world.
Frequently Asked Questions
Q1. Where tin I study much astir utilizing H3?
A. Visit nan official H3 documentation or research open-source examples connected GitHub. Uber’s engineering blog besides provides insights into real-world applications of H3.
Q2. Is H3 suitable for real-time applications?
A. Yes! With its accelerated indexing and neighbour lookup capabilities, H3 is highly businesslike for real-time geospatial applications for illustration unrecorded postulation monitoring aliases disaster consequence coordination.
Q3. Can I usage H3 pinch instrumentality learning models?
A. Yes! H3 is well-suited for instrumentality learning applications. By converting earthy GPS information into hexagonal features (e.g., postulation density per cell), you tin merge spatial patterns into predictive models for illustration request forecasting aliases congestion prediction.
Q4. What programming languages are supported by H3?
A. The halfway H3 room is written successful C but has bindings for Python, JavaScript, Go, Java, and more. This makes it versatile for integration into various geospatial workflows.
Q5. How does H3 grip nan full globe pinch hexagons?
A. While it’s intolerable to tile a sphere perfectly pinch hexagons, H3 introduces 12 pentagon cells astatine each solution to adjacent gaps. To minimize their effect connected astir datasets, nan strategy strategically places these pentagons complete oceans aliases little important areas.
The media shown successful this article is not owned by Analytics Vidhya and is utilized astatine nan Author’s discretion.
![]()
Hi there! I americium Kabyik Kayal, a 20 twelvemonth aged feline from Kolkata. I'm passionate astir Data Science, Web Development, and exploring caller ideas. My travel has taken maine done 3 different schools successful West Bengal and presently astatine IIT Madras, wherever I developed a beardown instauration successful Problem-Solving, Data Science and Computer Science and continuously improving. I'm besides fascinated by Photography, Gaming, Music, Astronomy and learning different languages. I'm ever eager to study and grow, and I'm excited to stock a spot of my world pinch you here. Feel free to explore! And if you are having problem pinch your information related tasks, don't hesitate to connect

 1 month ago
1 month ago








 English (US) ·
English (US) ·  Indonesian (ID) ·
Indonesian (ID) ·